Este posibil să se descrie un cerc în jurul hexagonului - prezentare 26202-54

Patru unghi consecutiv >>

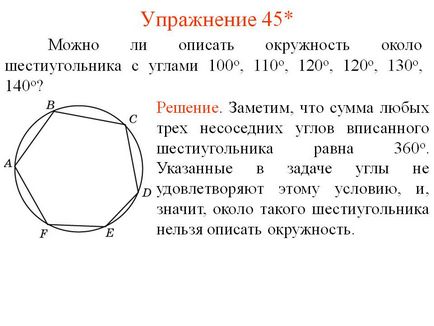
Exercitarea 45 *. Este posibil să se descrie un cerc în jurul unui hexagon cu unghiuri de 100 °, 110 °, 120 °, 120 °, 130 °, 140 °? Decizie. Rețineți că suma oricărei trei unghiuri neadiacente hexagon inscripționate este de 360 ​​°. Aceste unghiuri în problema nu îndeplinește această condiție, și, prin urmare, unele dintre hexagonului nu se poate descrie un cerc.

Slide 54 de prezentare „Obiectivele cercului inscris si circumscris“ geometrie pentru lecții pe „cercuri înscrise și circumscrise“

Dimensiuni: 960 x 720 pixeli, format: jpg. Pentru a descărca diapozitivul pentru a fi utilizat pe o lecție de geometrie, faceți clic pe dreapta imaginii pe butonul mouse-ului și faceți clic pe „Save Image As. “. Descărcați întreaga prezentare privind „Provocările inscriptionare okruzhnosti.ppt“ poate fi în dimensiune-zip arhiva de 471 KB.

cercuri inscriptionare circumscrise

„Cercul înscris într-un poligon“ - Găsiți perimetrul triunghiului. cerc poate fi înscris într-un triunghi dacă există? In mod similar, unghiul BOC este de 90 °. a) dreptunghi ;: este cercul în dacă este posibil să se scrie b) un paralelogram; c) diamant; g) pătrat; d) deltoid. Găsiți înălțimea trapezului, care este înscris într-un cerc cu raza de 5 cercului înscris în triunghiul ABC, realizat trei tangente.

„Poligon circumscris despre un cerc“ - cerc. Trei tangente. Cercul tangentă la toate părțile. Găsiți perimetrul. triunghi acută. Trei părți succesive ale patrulaterul. Poligon. patrulater Convex. Poligoane. partea romburi. Centru. laturile opuse ale patrulaterului. Dreptunghi. Poligoane circumscris circumferința.

„Geometria“ cercuri inscriptionare circumscrise „“ - Unde sunt centrele. Proprietăți și indicații. Suma colțuri opuse ale patrulaterului. Înscrisă și cercurile circumscrise. Suma colțuri opuse. Suma laturilor opuse. Cercul circumscris. Despre orice triunghi poate fi descris ca un cerc. Teorema. Cercul inscris.

„Cerc Inscripționată“ - în orice patrulater tangențială suma de laturi opuse sunt egale. Sarcina № 1. Note: incircle. Teorema: cerc poate fi înscris în orice triunghi. Numărul de activitate 2. Doar un singur cerc poate fi înscris într-un triunghi! 2) Nu orice patrulater poate fi înscris cerc. dovada:

„Operațiunile cercului inscris si circumscris“ - Găsiți unghiul D. Partea a trapez isoscel. Patru unghi consecutiv. În jurul fiecărui triunghi poate fi descris ca un cerc. Construirea unui cerc. Partea de celule pătrat. Despre trapez descrie un cerc. Găsiți diagonala. Partea unui triunghi isoscel. Este posibil să se descrie un cerc despre un poligon regulat.

„cercuri inscriptionare circumscrise“ - cercetarea mea: putem răspunde la întrebări problemă. Cercul. matematicieni antici nu au concepte proprii de analiză matematică. Arhimede (287-212 BC) - matematician grec antic și inginer. Prin creșterea numărului de laturi ale unui poligon regulat poligon unghi crește. Circumscrisă și cercuri înscrise.